Главная » Мануалы

1 ... 3 4 5 6 7 8 9 ... 33

Аналогично для расчета индуктивности цилиндрической намотанной секции с выступающими обкладками (безьшдук-ционная намЬтка) можно воспользоваться формулой для вычисления индуктивности короткого проводника круглого сечения (рис. 25)

(1-71)

где / - длина секции и D - ее диаметр.

i .-J

Рис. 25. К расчету индуктивности цилиндрического конденсатора

с безындукционной намоткой.

Правильность формул (1-70) и (1-71) для расчета индуктивности конденсаторных секций в двух рассмотренных случаях была подтверждена экспериментальной проверкой.

Расчет индуктивности выводов конденсатора и его межсекцйонных соединений

Для расчета индуктивности выводов и внутренних соединений в конденсаторах могут быть применены имеющиеся в литературе формулы, соответствующие ряду токопроводящих конфигураций, которые встречаются в конструкциях конденсаторов или сходны с ними. При использовании в конденсаторе проводников круглого сечения применяются формулы, соответствующие одиночному прямому проводнику или двум параллельным проводникам круглого сечения (рис. 26, а и б).

Для одиночного проводника круглого сечения может быть использована формула (1-71).

Для двух параллельных проводников круглого сечения

(1-72)

Если длина проводника много больше его радиуса и расстояния между осями проводников, т. е. если / > г и / > d, формула упрощается

(1-73)

При использовании в качестве выводов или межсекцион-ных соединений конденсатора плоских шин прямоуголь-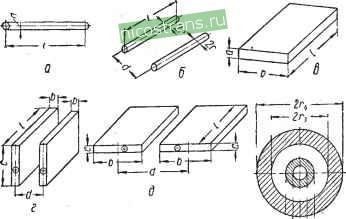

<-12л'-4

е

Рис. 26. К расчету индуктивности выводов конденсатора:

а - одиночный проводник круглого сечения; 6 - два параллельных проводника круглого сечения; е - одиночная шина прямоугольного сечения: а - параллельные шины, сближенные широкими сторонами; й -две параллельные шины, сближенные узкнмн стбронами; е - коаксиальный кабельный вывод.

НОГО сечения или полосок металлической фольги, могут быть применены формулы, соответствующие конфигурациям на рис. 26 е, г и д.

Для одиночной шины прямоугольного сечения можно применить формулу (1-70).

Для двух параллельных шин прямоугольного сечения, сближенных широкими сторонами (при с > Ъ),

+In (1 \-f) + ~ arctg t] , (1-74)

где T =

Для двух параллельных шин прямоугольного сечения, сближенных узкими сторонами (при с < Ъ),

1п(Р + 1) +

(1-75)

где Р = .

При высоких частотах можно предполагать, что ток распределяется практически равномерно вдоль широкой стороны сечения каждой из шин и принять в формуле (1-74) b = О, а в формуле (1-75) с = 0.

Если вывод конденсатора осуществлен отрезком коаксиального кабеля с полым внутренним проводником (рис. 26, е), то

2Л

Ь 2 2

(1-76)

Если внутренний проводник имеет сплошное сечение, т. е. = О, то

fig/

2п

1 + 21пй +

. (1-77)

При высоких частотах можно принять, что весь ток будет вытеснен к наружной поверхности; т. е. Гз = г^, тогда

(1-78)

При расчете индуктивности выводов от плоскопрессованных намотанных секций, имеющих вид полосок медной луженой фольги, выпущенных с одного торца секции, Г. С. Кучинский и К. М. Иркаева применяли следующие формулы:

а) при смещении выводов в пределах ширины секции (рис. 21, а) для индуктивности каждого из них - формулу (1-67), представляющую собой упрощенный вариант формулы (1-70) для проводника прямоугольного сечения, когда а С fc и Ъ < I. При этом для формулы (1-67)

принималось, что Iab - длина вывода, выступаюнщя за пределы обкладок секции, b - ширина вывода;

б) при смещении выводов на половину витка и расположения их друг под другом (рис. 21, б) для индуктивности обоих выводов - формулу (1-64), соответствующую плоскому конденсатору с двумя параллельными обкладками. В этом случае: - толщина вывода, / - длина выюда (за пределами обкладок конденсаторной секции), b - ширина вывода и а - расстояние между выводами.

Пример 1. Рассчитать суммарную индуктивность плоскопрессованной секции высоковольтного бумажного конденсатора при следую- щих данных: С = 1 мкф, толщина диэлектрика d = 80 мк, толщина фольги dф = 10 мк, ширина фольги b = 280 мм, ширина выводного контакта 10 мм, длина его 50 мм; контакты сдвинуты по длине фольги обкладок на 100 мм (в пределах ширины секции).

Принимаем, что индуктивность состоит из трех слагаемых: Li - индуктивность основной части секции с бифилярной намоткой; La - индуктивность обкладок на длине, расположенной между сдвинутыми выводами, т. е. на участке, где токи в обкладках совпадают; Ls - индуктивность выводов.

Для определения Li надо знать длину фольги в секции, которую определяют по формуле (1-46):

Cd 1-80

~ 0.177£б ~ 0,177 3.5 28 ~

Здесь для пропитанной бумаги (предположена неполярная пропитка и небольшая плотность бумаги) принято е = 3,5. Длина фольги полу- чена в м, поскольку d - вмк, Ь - всжиС-в мкф.

Зная длину фольги, вычитаем из нее часть длины между выводами: 460 - 10 = 450 см. Находим индуктивность этой (бифилярной) части обкладок по формуле (1-65):

Li = i?ll--lj-i(2 . 10 10-4 -f 3 80 10-4) = 1.8 10-8 гн.

Индуктивность части обкладок между выводами находим по фор-vMyfle (1-67):

4jt. 10- 10 f 1 , 2 10 , Л

Индуктивность одного вывода находим по той же формуле (1-67). Для двух выводов получаем

Таким образом, L = (1,8 -Ь 3 -Ь 56) Ю = 60,8 Ю гн, причем основная часть индуктивности приходится на долю выводов.

Пример 2. Определить индуктивность цилиндрического намотанного конденсатора с выступающей фольгой диаметром 15 мм к длиной 50 мм, имеющего осевые выводы, выполненные проводником диаметром 1 мм и длиной 40 мм (с. каждой стороны).

Индуктивность тела конденсатора находим по формуле (1-71):

1ИМ индуктивность двух выводов

по той же формуле находим индуктивность двух выводов

, 2 4л . 10-

Ч=-2-

Суммарная индуктивность

L = (16 + 65) 10- = 81 10-8 гн.

И в этом случае выводные проводники обусловили большую часть общей индуктивности.

Приняв, что емкость конденсатора равна 0,5 мкф, найдем для него резонансную частоту

= -7= =- = 2.1 10в гц = 2.1 Мгц.

Р 2кУьС 2Jt/8,1 10-8.0,5- 10-

Пример расчета индуктивности конденсатора высокого напряжения плоской конструкции, собранного в железном баке, дается в работе П. Н. Дашука.

§ 5. РАСЧЕТ ПОТЕРЬ В КОНДЕНСАТОРАХ

Активная мощность Ра. выделяемая в конденсаторе в виде тепла, определяется потерями в диэлектрике и потерями в металлических частях конденсатора:

Ре.==Р„ + Р . (1-79)

При учете потерь в диэлектрике необходимо прежде всего вычислить потери в основном диэлектрике конденсатора. Если тангенс угла потерь основного диэлектрика составляет tg6o, емкость, определяемая основным диэлектриком. Со и к конденсатору приложено напряжение U частоты /, то

Pд = 2lv ==Cotg8o, (1-80)

где Рд-в вт, f - в гц, U - в в и Со - в ф.

Кроме потерь в основном диэлектрике есть потери и во вспомогательных диэлектриках (выводные изоляторы, заливочная масса, изоляция от корпуса, материал корпуса, если

I 59

последний изготовлен из электроизоляционного материала, пластмассовая опрессовка и т. д.). Величина этих добавочных потерь определяется соответствующей паразитной емкостью Сп, создаваемой электрическим полем рассеяния, которое проходит через вспомогательный диэлектрик, и тангенсом угла потерь диэлектрика tg6n:

Яд oc==2/[/-Cntg8 . (1-81)

Обычно величина Сп относительно невелика в сравнении с основной емкостью конденсатора Со и теряемая в ней мощность мала, поэтому при расчете общих потерь в конденсаторах потери во вспомогательных диэлектриках можно не учитывать. Однако при изготовлении конденсаторов небольшой емкости из диэлектрика с малым tgfip с использованием вспомогательных диэлектриков с большим tg6n пренебрегать потерями Яд. доп уже нельзя. В этом случае, используя выражения (1-80) и (1-81), получаем выражение для суммарных диэлектрических потерь в конденсаторе

я; = 2r.fU (Со tg 8о + f Сп, tg 8п,), (1-82)

где под знаком суммы учитываются потери в различных видах вспомогательной изоляции. При расчете надо знать значения емкостей Сп, которые трудно точно рассчитать и проще определить экспериментально на макете конденсатора. В небольших конденсаторах значения Сп обычно не превышают нескольких пикофарад, но в больших конденсаторах, в частности для емкости, обусловленной изоляцией от корпуса, могут достигать сотен и тысяч пикофарад.

Так как значение Со определяется только основным диэлектриком, т. е. равно фактической емкости конденсатора С - Сп, а обычно Сп < Со, то можно принять Со = С, т, е. полной емкости конденсатора.

Потери в металлических частях конденсатора определяются прежде всего потерями на нагрев обкладок и выводов. Если выюд соединен с обкладкой с помощью вкладного контакта, который не припаян или не приварен к обкладке, то могут появиться потери в переходном сопротивлении контакта между обкладкой и выводом; обычно этими потерями можно пренебречь. Они могут сказываться в тех случаях, когда после воздействия влажности или иной причины

Ij-XXO-X-L-L-L-LX-L

т-тттгтт-г-гтт

переходное сопротивление возрастает вследствие появления окиси на металлических поверхностях в месте контакта.

Для электролитических конденсаторов понятие потери в металлических частях надо понимать условно, так как в таких конденсаторах одной из обкладок служит электролит; подсчитывая потери в обкладках, приходится учитывать потери в слое электролита. Этим объясняется высокое значение tg6 электролитических конденсаторов.

Учитывая только потери в обкладках и выводах, получаем

(1-83)

где Рм - в вт, при / - в а и г - в ом.

Величину /- можно назвать общим сопротивлением металлических частей конденсатора.

При расчете потерь в обкладках надо учитывать, что плотность тока в обкладках не одинакова по их длине; ток спадает

от контакта вывода с обкладкой к концу обкладки. Рассмотрим плоский конденсатор, полученный разверткой намотанного конденсатора с вкладными контактами, поставленными в самом конце намотки; шириной контакта пренебрегаем. Обозначим длину обкладки / см, ширину b см и толщину do см (рис. 27). Удельное сопротивление материала обкладки р ом-см, полный ток, потребляемый конденсатором, / а. Если в начале обкладки ток равен /, то к концу обкладки он спадает до нуля (рис. 27, вверху). На расстоянии х от конца обкладки выделим элемент обкладки длиной dx, в котором значение тока будет 1. Мощность, рассеиваемая в этом элементе.

Рис. 27. К расчету потерь в обкладках при вкладных выводах, помещенных в начале или в конце намотки.

dP = IxP

(1-84)

Значение тока Ix будет меньше полного тока / во столько раз, во сколько х меньше I, т. е.

/. = /f. - (1-85)

Подставляя значение 1 в формулу (1-84), получим

Pbd.

(1-86)

Для нахождения полных потерь в обеих обкладках надо взять интеграл от выражения (1-86) в пределах от нуля до Z и удвоить полученное значение:

Р Г., 2 го. I

(1-87)

Если обозначить Ро = /Vo, где под Гд понимать приведенное значение сопротивления обкладок, учитывающее неравномерность распределения плотности тока по длине обкладки, то используя выражение (1-87), можно написать

Таким образом, когда ток вводится в самом начале обкладок, приведенное сопротивление их, учитывающее спадание тока по длине обкладки, буде в 3 раза меньше, чем величина сопротивления, рассчитанная в предположении, что вся длина обкладки обтекается полным током /. Если поставить выюды в середине длины обкладки (рис. 28, а), то в начале каждой половины длины обкладки ток будет иметь половинное значение, которое спадает до нуля к концу этой половины обкладки. Учитывая эти соображения, получаем

и

1111 I

г

Рис. 28. Снижение потерь рациональным размещением выводов:

а - одна пара выводов в середине длины обкладок; б - несколько пар выводов.

Таким образом, при установке выводов в середине обкладки приведенное значение сопротивления обкладок, а следовательно, и потери в них Ро снижаются в 4 раза.

Еще больше снизить потери можно, применив несколько пар контактов, поставленных равномерно по длине обкладки (рис. 28, б).

Тогда

6 2 V bd

(1-90)

где n - числр пар контактов.

При использовании, например, 5 пар контактов потери в обкладках снижаются в 25 раз, в сравнении с одной парой в середине намотки, или в 100 раз, в сравнении с одной парой контактов в начале намотки. Однако это справедливо лишь при равномерном распределении тока между парами контактов, когда частота невелика и индуктивность обкладок и выводов еще не влияет на величину тока.

Резко снизить потери в обкладках можно при намотке с выступающей фольгой (безындукционной). В этом случае (рис. 29) длиной пути тока служит ширина обкладок bo, а шириной пути тока - длина I. Учитывая это, по аналогии с формулой (1-88) получаем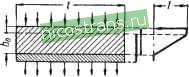

Рис. 29. К расчету потерь при безындукционной намотке (со сдвинутой фольгой).

(1-91)

Величина Го в данном случае уменьшается в отношении -j , по сравнению с намоткой со скрытой фольгой йодной

парой контактов в начале намотки. Отношение в обычных намотанных конденсаторах большой емкости может быть порядка 100; при этом потери в обкладках при переходе от намотки со скрытой фольгой к намотке с выступающей фольгой могут быть снижены в 10 ООО раз.

Формула (1-91) не учитывает закраину фольги АЬ, в которой ток имеет постоянное значение. Уточненная формула имеет вид

/-о-2р

A6 + f Id

(1-92)

Для намотанных металлизованных конденсаторов (ме-таллобумажных или пленочных) можно применять формулу (1-92). Поскольку в этом случае трудно определить толщину

слоя металла и его удельное сопротивление, удобнее использовать при расчетах значение Гсп в омах, рассчитанное на единицу поверхности. В этом случае

Ab + f I

/-о = 2Гел-j. (1-93)

Для плоского многопластинчатого конденсатора (рис. 30), например для слюдяного конденсатора с числом элементов М, активной длиной обкладок 4 и шириной закраины по длине А/, при ширине обкладок b и толщине do. Го можно вычислить по формуле (1-88) с учетом следующих замечаний.

Конденсатор состоит из М параллельно соединенных емкостей, на каждую из которых приходится полного тока конденсатора /. По каждой из крайних обкладок ток подводится только к одной из элементарных емкостей; таких обкладок будет две. По каждой из остальных УИ - 1 обкладок должен подводиться ток к двум элементарным емкостям, т. е. в обкладку будет входить

ток 2-. В каждой обкладке ток

проходит элемент длины AZ, не изменяясь по величине, а затем на длине /о спадает до нуля. Учитывая эти соображения, запишем выражение для полных потерь в обкладках многопластинчатого конденсатора

P, = [2(i) + ,A,-l)(f)-](A, + )4 =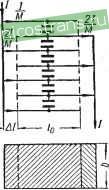

Рис. 30. К расчету потерь в многопластинчатом конденсаторе.

= г

,4М - 10

Л/4--

Поделив обе части полученного уравнения на Р и вы-неся за скобку ~, получим выражение для приведенного значения сопротивления обкладок

2М - 5 р о -f ЗА/

(1-94)

1 ... 3 4 5 6 7 8 9 ... 33