
 | |
 |
Главная » Мануалы 1 ... 4 5 6 7 8 9 10 ... 33 Для цилиндрического конденсатора (рис. 31), например трубчатого керамического конденсатора, используя приведенные выше соображения и выразив ширину обкладки как среднюю длину окружности (Dcp - среднее значение диаметра конденсатора), получим + (1-95) /о == Если конденсатор имеет вид плоского диска, например керамический дисковый конденсатор (рис. 32), причем подвод тока осуществляется в центре с помощью проводника радиусом Г1, а об-кладка представляет собой 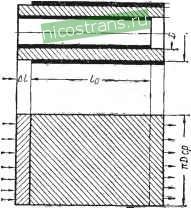 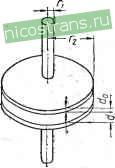 Рис. 31. К расчету потерь в цилиндрическом конденсаторе. Рис. 32. К расчету потерь в дисковом конденсаторе с подводом тока в центре обкладки. круг радиусом Гг. то сопротивление обкладок можно вычислить по формуле, предложенной Л. 3. Гоголицыным, Го == 2itrf  (1-96) где do - толщина обкладки. В сухом намотанном электролитическом конденсаторе сопротивление обкладок определяется сопротивлением волокнистой прокладки, пропитанной электролитом (рис. 33). -Если длина анода I, ширина b и толщина прокладки, про- 5 592 питанной электролитом, d p (размеры в см), то при удельном сопротивлении электролита Рэл {ом см) и коэффициенте проницаемости прокладки <р (учитывающем увеличение сопротивления электролита при его впитывании в прокладку) получаем значение сопротивления обкладок 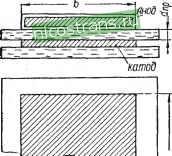 Го =<РРэл (1-97)
в данном случае путь тока равен толщине, прокладки, так как благодаря использованию катодной фольги ток подводится к прокладке по всей ее поверхности. Рассмотрим примеры расчета сопротивления обкладок. Пример 1. Вычислить сопротивление обкладки намотанного кон- -денсатора. при длине фольги 5 м, ширине 50 мм и толщине 5 мк; фольга - алюминиевая (ряЗ ж/сол см). Намотка - со скрытой фольгой, контакты вложены в Середине намотки. Используем формулу (1-89): Рис. 33. К расчету потерь в электролитическом конденсаторе. з-ю- 5 10)- 5-5 = 0,1 ом. 10-4 Пример 2. Вычислить сопротивление обкладки аналогичного конденсатора, но при намотке с выступающей фольгой, полагая, что активная ширина 50 мм и величина закраины 3 мм; длина и толщина обкладки те же, что в примере 1. Используем формулу (1-92): 0.3--!- = 2 . 8 . 10-е . ПоГ-5Г[о-4 = 4.7 . 10- ом. Сопротивление обкладок при переходе к намотке с выступающей фольгой по сравнению с предыдущим примером снизилось примерно в 2000 раз. Из приведенных примеров видно, что сопротивление обкладок относительно невелико, а потому при низкой частоте, . когда конденсатор потребляет небольшой ток, потери в обкладках малы. G ростом частоты потери юзрас- тают, так как ток резко увеличивается. Так, при токе 10 а потери в обкладках в примере 1 (Го = 0,1 ом) составляют 10 вт. При таком же токе в примере 2 потери составляют всего лишь 4,7 мет, т. е. практически не ощутимы. В связи с тем что обкладки в конденсаторах обычно имеют малую толщину (от 15-25 мк до малых долей микрона), влияние поверхностного эффекта на их сопротивление не учитывается. Потери в выводах конденсатора определяются сопротивлением выводных проводников, которое легко подсчитать, если известно удельное сопротивление материала, длина вывода и его сечение, Гвыв = 9ом. (1-98) Длина I - в см, площадь сечения S - всм^ и р -в ом см. Если конденсатор имеет два изолированных вывода, то сопротивление, вычисленное по формуле (1-98), надо удвоить. Для выводного проводника круглого сечения с диаметром D г^ш-=р^,. (1-99) При высоких частотах сопротивление вывода возрастает за счет поверхностного эффекта, вызывающего неравномерное распределение плотности тока по сечению проводника вследствие вытеснения тока к поверхности. Глубина проникновения тока в металл, считая от его поверхности, характеризуется величиной А, определяющей расстояние от поверхности, на котором амплитуда тока убывает в е раз, А = ]/ -. (1-100) где р - удельное сопротивление металла; [i - магнитная проницаемость; f - частота; k - постоянный коэффициент. При расчетах сопротивления проводников на высокой частоте за эффективную площадь сечения можно принимать произведение Aif, где г); - периметр проводника. Для круглых проводников было предложено учитывать Возрастание сопротивления при высоких частотах путем 5* .67 умножения /-выв на поправочный коэффициент F{aj. Для немагнитного материала a = 0,1407D (1-101) где D - диаметр, см; f - частота, гц; Р - удельное сопротивление, мком-см. Формулу (1-101) можно представить иначе: oi = kDVJ. (1-102) Коэффициент k для меди равен 0,106, для серебра - 0,111 и для алюминия - 0,0843. Значения F{a) при разных значениях а:
При а > 3,0 величину F{a) можно найти по приближен-иой формуле < E( );l%hL. (моз) Полные потери в конденсаторе Ра = Рд + Рм = 2fU (С tg 8о + tg 8ш) + /V . (1-104) Здесь Гм = Го -h / выв^значение Со, входившее в формулу (1-82), заменено значением С, т. е. полной емкостью между выводами конденсатора. Разделив выражение, стоящее в скобках, на С, получим tg8o + 5]%4g8 - = tg8 . (1-105) Это выражение представляет собой составляющую тангенса общих потерь конденсатора, соответствующую только диэлектрическим потерям (в основном во вспомогательных диэлектриках). Подставив в последний член выражения (1-104) значение тока, выраженное через напряжение, частоту и емкость, получим /.Vm = iTCr == 2ф'е 21г/С/-м = 2ф'С tg 8 . (1-106) Здесь tg6 = 2я[Сга представляет собой составляющую тангенса общих потерь конденсатора, соответствующую только потерям в металлических частях конденсатора (в обкладках и выводах). После преобразований выражение (1-104) имеет следующий вид: Ра = 2fUC tg 8д + 2fUC tg К = 2fUC (tg 8д + tg 8 ). (1-107) Обозначая tg6 = tgбд + tg6 , где б-есть общий угол потерь конденсатора, учитывающий все потери в последнем, получаем: Pa = 2ir/f;=ctg8, {i-my где Ра - в вт, f - в гц, U - ввиС - в ф. Если рассчитывается конденсатор определенного типа, аналогичного уже выпускавшимся на производстве с нормированным значением tg6, то потери по их составляющим элементам можно не вычислять, а сразу найти общие потери по формуле (1-108), используя в ней нормированное значение tg6. При этом надо брать наибольшее допускаемое нормами значение, соответствующее верхнему пределу температуры, для которой ведется расчет. Значения tg6, допускаемые отечественными ГОСТ или ТУ для некоторых типов конденсаторов с твердым диэлектриком, приведены в табл. 2. Следует отметить, что формула (1-108) получена для синусоидального напряжения. Если кривая напряжения отличается от синусоидальной, т. е., кроме основной синусоиды с частотой fi, содержит также синусоиды высших частот (высшие гармоники), то величина,Ра может заметно юзрасти. В' этом случае общие потери конденсатора представляют собой сумму потерь от каждой отдельной гармоники. Для k-й гармоники с частотой (угловая частота = = 2nf - 2nkfi = kwi) значение потерь, вызываемых ею в конденсаторе, Paft=i7Kctg8,=.Ktg8,. Здесь взято значение tgS;, так как угол потерь зависит от частоты. Значения tg& конденсаторов с твердым диэлектриком, допускаемые отечественными нормами
где тг] V Суммарные потери от п гармоник Ра = S Paft = o)iC S kVl tg Ik = -rjcoiCi; tg 8 (1-109) коэффициент возрастания потерь за счет наличия высших гармоник; действующее значение несинусоидального напряжения, которое равняется корню квадратному из суммы квадратов напряжений всех гармонических составляющих: VVv\-V\V\-V ... Vl. (1-110) Значение коэффициента К] можно вычислить по формуле = %tgs, -Sbfeb (Mil) где Если в рассматриваемой области частот-угол потерь мало зависит от частоты, то можно положить bk = 1 и вычислить значение к] как сумму членов kal, т. е. воспользоваться формулой (1.И2) ul+ ... +UI+ ... +ul Для вычисления т) заданную кривую напряжения раскладывают в ряд Фурье и находят напряжения отдельных гармоник. Гармониками с очень малыми напряжениями можно пренебрегать. Пример. Вычислить г\ для кривой напряжения, показанной на рис. 34, а. При разложении этой кривой были получены: 1-я гармоника--100%, 3-я-28,5% и 5-я -5,0% (указаны относительные значения напряжения). При изменении частоты в пределах от 50 до 5 50 = 250 гц tg 8 для бумажного конденсатора (рассматриваемого в данном случае) меняется незначительно и можно Принять bk = I, Т. е. использовать формулу (1-112). Окончательно получим 1.0 - 3 0.285 - 5 0.05 ~ 1.02 - 0,2852 - 0.052 1 о- Таблица 3 Результаты вычисления tj для сильно искаженной кривой (рис. 34, б)
 6.0144 1.3928 = 4,33 Рис. 34. Искажение кривых напряжений при наличии высших гармоник: а - 3-й и, 5-й: б - до 17-19-й. Таким образом, в данном случае потери увеличиваются за счет искажения формы кривой напряжения только на 16%. При более сильных искажениях, особенно при наличии более высоких гармоник
(9-я, 11-я и т.д.), величина т) может быть много больше и доходить до значений т] 3 н- 5 и даже выше. В качестве примера приведем расчет коэффициента т) для кривой, форма которой показана на рис. 34, б. Значения напряжений высших гармоник (по отношению к 1-й гармонике, принятой за единицу), а также результаты вычислений приведены в табл. 3. Непосредственное измерение потерь в конденсаторе, к которому было приложено это сильно искаженное напряжение, проведенное А. К. Гер-циком и В. П. Матвеевой с помощью калориметрического метода, позволило найти экспериментальное значение т], которое оказалось равным 4,05, т. е. . достаточно близким к расчетному, указанному в табл. 3. Вопрос о потерях в конденсаторе при воздействии импульсных напряжений был рассмотрен в работе Пейссу, который дает ряд расчетных формул для вычисления активной мощности конденсатора при некоторых типичных формах импульсного напряжения. Для пилообразных импульсов, показанных на рис. 35, а, при амплитуде напряжения и и значениях Тих в соответствии с рисунком, имеем 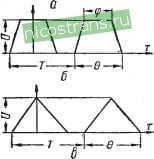 Рис. 35. К расчету потерь при различных формах импульсного напряжения: о -пилосбразной; б -трапецеидальной; в - треугольной. где 2х Для трапецеидальных импульсов (рис. 35, б) t/2coC tg й 0,78 где а=:-уг и (1-114) Для треугольных импульсов (рис. 35, в) можно применять формулу Pa = 5, (1-115) где а имеет то же значение, что и в предыдущей формуле. Значения tg6 для подстановки в эти формулы надо выбирать в соответствии с угловой частотой следования импульсов (0. Формулы (1-114) и (1-115) дают предельное значение мощности, рассеиваемой при данной форме импульсов (практически наблюдаемые значения будут несколько ниже). Эти формулы получены в предположении, что угол потерь н^ зависит от частоты в тех пределах, которые соответствуют высшим гармоникам, учитываемым при расчете. Для прямоугольных импульсов при разложении в ряд Фурье получается ряд такого вида, сумма членов которого стремится к бесконечности при неограниченном увеличении числа членов ряда. Следовательно, при строго прямоугольной форме импульса потери можно считать в конденсаторе бесконечно большими. Практически строго прямоугольная форма импульса не получается и его можно рассматривать как трапецеидальный, применяя для расчета потерь в конденсаторе формулу (1-114). Трапеция будет тем ближе к прямоугольнику, чем больше отношение <р к 6, т. е. чем больше величина г (рис. 35, б). В пределе при величине г - I согласно формуле (1-114) получаем Ра = со. Обычно трапецеидальные или треугольные импульсы, показанные на рис. 35, имеют не острые, а закругленные углы, что и дает снижение фактических потерь в сравнении с расчетными. Вопрос о вычислении потерь в конденсаторах при импульсном режиме рассмотрен также в работе Л. 3. Гоголи-цына. Он предлагает рассматривать действие одиночных зарядов и разрядов, разделенных длительными паузами, как действие непрерывной последовательности таких зарядов и разрядов, учитьшая скважность между ними при вычислении величины потерь. Если последовательность импульсов состоит из длительных зарядов и кратковременных разрядов, то ее можно представить в виде двух самостоятельных последовательностей, составленных из процессов одинаковой длительности. К каждой из таких последовательностей можно применить разложение в ряд Фурье, получив быстросходящиеся ряды, позволяющее легко вычислить потери. При этом каждая последовательность одних только зарядов или одних только разрядов должна заменяться непрерывным чередованием зарядов и разрядов, одинаковых по длительности. Это поясняется рис. 36. Кривая а, полученная чередованием длительного заряда (продолжительность Го -т])и кратковременного разряда (продолжительность т) заменяется кривыми бив; кривая б представляет собой чередование длительных зарядов и длительных разрядов, а кривая в - чередование кратковременных зарядов и кратковременных разрядов. Вели-чина tg6, используемая при расчете, выбирается в соответствии с частотой следования импульсов. Полученное значение потерь для учета скважности умножается на отношение вре-мени импульса к величине промежутка времени между импульсами. При этом учитьшаются в основном потери в диэлектрике конденсатора. В импульсных конденсаторах высокого напряжения, формирующих кратковременные импульсы большой мощности, проходят большие импульсные токи, которые, несмотря на их кратковременность, могут дать заметное выделение тепла в конденсаторе. Кривая изменения тока в импульсном конденсаторе приведена на рис. 36, г. Для вычисления потерь в обкладках, обусловленных импульсными токами, Л. 3. Гоголицын предлагает формулу 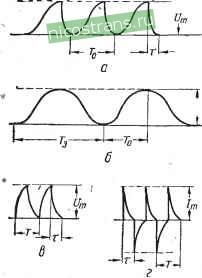 Рис. 36. К расчету потерь по методу Гоголицына: а - длительный заряд и кратковременный разряд; б - длительный заряд н длительный разряд; в - кратковременный заряд и кратковременный разряд; г - кривая изменения тока в импульсном конденсаТ1ре. (1-П6) где q - скважность; Го - приведенное сопротивление обкладок (вычисляемое по приведенным выше формулам); 1 ... 4 5 6 7 8 9 10 ... 33 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||