
 | |
 |
Главная » Мануалы 1 2 3 4 5 6 ... 22 На третьем этапе декодирования, когда известны все значения локаторов, ошибки определяются из системы уравнений синдромов ошибок (1.9). Для этого система уравнений (1.10) записывается и решается в матричной форме где
- матрица компонентов синдромов ошибок. Если матрица M{S) не вырождена, то система (1.14) имеет решение = M-i (S)- -5, - Sr+i (1.15) Матрица вырождена, если ее определитель detM(S) не равен .нулю. При этом число строк матрицы равно числу ошибок. Итеративный метод решения уравнения (1.15) заключается в том, что последовательно принимаются значения ошибок от r=f до г=0 и каждый раз вычисляется определитель матрицы M(S), пока не будет получено значение определителя, отличное от нуля. Таким образом определяется действительное число ошибок в блоке. Когда это число известно, из (1.15) рассчитывают коэффициенты а многочлена локаторов ошибок (1.11). Если степень этого многочлена 1 или 2, то его корни находятся по известным формулам, как это делается при решении уравнений первой и второй степени. В общем случае простейшим путем нахождения корней является метод проб и ошибок, известный как процедура Ченя . Когда определены все локаторы ошибок, их можно подставить в систему уравнений (1.9). Эта система решается путем обращения матрицы локаторов ошибок (1.16) Частные решения для нуля, одной и двух ошибок приведенных систем уравнений называются прямым алгебраическим мето-
дом декодирования. Этот метод для кода CIRC наиболее оптимальный, поэтому рассмотрим его подробнее. Обозначим оши-боч'ные символы е, а безошибочные е. Если символы не имеют флагов стираний, то их обозначают ео и во, а если имеют - то Ef И е/. Сначала рассмотрим исправление только ошибок без использования стираний. Важнейшим этапом декодирования является идентификация, в процессе которой декодер принимает решение о числе ошибочных символов в блоке, и в соответствии с этим решением устанавливается определенный алгоритм (подпрограмма) работы декодера. Идентификация может производиться в виде отдельной операции или в неявном виде в процессе локализации и исправления ошибок. При прямом методе декодирования идентификация осуществляется с использованием математических критериев, которые получаются при решении систем уравнений (1.9) - (1-11). Для кода CIRC возможны лишь три случая: 1) нет ошибок, г=0; 2) одна ошибка, г-=\; 3) две ошибки, г=2. Результаты решений систем уравнений для этих случаев приведены в табл. 1.1. Если г=0, то из решения системы (1.10) следует основное условие отсутствия ошибок в блоке 5o = Si = 52 = S3 = 0. (1.17) Если г=\, то из решений тождеств Ньютона (1.10) получаем другие условия одной ошибки в блоке: X. = а', = Si/5o = SjSi = SJS; oi ii St Sg 0 ; A = S,S + S\ = Q; 5 = 5iS2-fSoS3 = 0; CSS + Sl (l- Если r==2, TO для того чтобы многочлен локатора ошибок имел два не равных нулю корня, необходимо выполнение условий 5о и 5i и 5 и 5з#0, Л,5,С#0. (1.19) Так как код RC в обеих ступенях укороченный, что позволит ввести дополнительное условие проверки числа ошибок в блоке, выполняемое на стадии локализации ошибок в блоке, путем проверки выполнения неравенства i,/<rt-l. При наличии ошибок в блоке всегда возможны комбина-дии, когда одни ошибки в уравнении синдромов компенсируют другие, а в результате один или несколько синдромов сразу получаются равными нулю. Поэтому приведенные критерии не являются абсолютными. Даже при равенстве нулю всех четырех синдромов не исключается наличие в блоке ошибки, которую декодер не обнаружил. Таким образом, идентификация может 26 Таблица 1.1. Результаты решений систем уравнений (1.9) и (1.10) для кода RC Тождество Ньютона (2-3) Oj- (2-3) а (г) (2-5) Критерий идентификации
Sn Si, S2, S3 - 0 или So = 0, S3 = 0 So Si Sa 0(г) = = Z-f0fi So, Si, S2, S3 ?;0 Л=В=С=0 i < re - 1, где Л = S -f So Sa В = Si Sa -b So S3 С = Si S3 50 = Si + Ё2 51 = xisi -\- x2 82 52 = 1 81 62 53 = Xj 61 -- Eg 82 50 a24-Si ori+S2=0 51 a2+S2 Oi-fS3=0 0, = -- = D a, = -- = £ a(z) = z + -f 01 г -f 02 Xl = a -ojx ai =aJY где 1-f a 8, = %So + Si Xi-f X2 61 = 80 -f 82 SoUSiUSUSjsO A, B, CO быть правильной или неправильной с определенной вероятностью, которая зависит как от критериев идентификации, так и от числа используемых проверочных символов i[10]. Идентификация считается правильной, если блок с r{rt) ошибками идентифицируется как блок с таким же числом ошибок 1{1=г) и производится их исправление, а также если блок с r{r>t) ошибками идентифицируется как блок с числом ошибок более t и производится отказ от декодирования. Идентификация считается неправильной, если блок с r>t ошибками идентифицируется как блок с Ist ошибками при г> либо как блок с l¥=t ошибками при г^г . Неправильная идентификация всегда сопровождается сложным исправлением ошибок, при котором число ошибок на выходе декодера становится больше, чем на входе. Определение локаторов одиночных ошибок производится в соответствии с равенством, которое следует из решения o-(z)=0: x, = a = Si/So. (1.20) В случае двойных ошибок получить аналитическое выражение для корней квадратного уравнения в поле Галуа 2-fOiZ-f а, = 0 не представляется возможным. Для решения таких уравнений пользуются целым рядом искусственных приемов. Один из них - определение корней с помощью таблицы, хранящейся в памяти декодера. С этой целью вводится дополнительная переменная Q, связанная со значением локаторов ошибок i и / равенством j = i + Q- Известно, что для приведенных квадратных уравнений в поле Галуа справедлива теорема Виета о корнях а' и а', в соответствии с которой ах = а^ + а^ о^ - а^-а', где (Т1=5/Л, G2 = C/D. После замены переменных } = i + Oi = B/AD, а^ = С/А^Е. Исключая /, получаем выражение D/E = BVAC = a-° + a, где переменная Q однозначно определяется синдромами ошибок. Расчетные формулы локаторов ошибок могут быть приведены к виду Xl = а' = Oi/X, х^ = а' = ojY, где Х=\+а^, У=1--а-. Таблица данных строится как зависимость Q от В^/АС или сразу в виде зависимости \ + а^ и 1+а~° от В^/АС. 2в Когда определены локаторы ошибок, их значения рассчитывают по формулам: при 7- = 1 8 = So; при г = 2 е^- = 82 = (а' So + Si)/(a + а') = {х^ Sq + Si)/{x + х,); Ej - вд = Sq -f- 2 На рис. 1.8-1.11 приведены алгоритмы, поясняющие прямой метод декодирования кода RC с исправлением одиночных и двойных ошибок. Рассмотрим исправление ошибок и стираний в коде RC. Стертыми символами могут быть как ошибочные е, так и безошибочные е. Обычно стирания вводятся в первой ступени декодирования кода CIRC, в частности, когда число ошибок в блоке превышает исправляющую способность первой ступени декодирования. Стирания могут вводиться при обнаружении ошибок в декодере канального кода EFM. Возможно введение стирания и при исправлении двойных ошибок, когда вероятность правильной идентификации мала. Когда декодер может исправлять ошибки или стирания, а также ошибки и стирания одновременно, его исправляющая способность существенно возрастает, но при этом увеличивается также сложность декодера. В коде CIRC в каждой ступени могут быть исправлены до четырех стираний, одна ошибка и одно стирание, а также два стирания и одна ошибка. В табл. 1.2 для этих случаев приведены системы уравнений синдромов. На основании этих систем вырабатываются критерии идентификации стираний и ошибок. Задача расчета локаторов ошибок возникает только при одновременном исправлении ошибок и стираний. Если в блоке имеется одиночное стирание (ошибка с флагом гр), то из системы уравнений синдромов следует Xl = a, а'SJSo = 82/81 = 5/8,. Поэтому критерием одного стертого ошибочного символа является вьшолнение условий о - Xi8q-\- 8i - О, S[=Xi8i + S2 = 0, г = 1 г ~Ь = О (1.21) и наличие одного флага в блоке {F=l), где So, Si, S2 являются модифицированными синдромами. Так как стирание в данном случае является и ошибкой, то критерии одной ошибки (1.21) также должны выполняться. Из системы уравнений табл. 1.1 видно, что в данном случае величина стертого символа определяется равенством 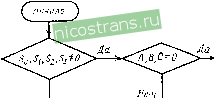 Нет Hem ошибок или более одной ошибна
более одной ошибки Начало 1 Определение локатора. I 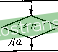 Нет Вычисление ошибки £j Коррекция ошибки Wi +£ j более одной ошибки Попей; Рис. 1.8. Алгоритм исправления одной ошибки (а) и алгоритм локализации и и коррекции одной ошибки (б)  Нет 
Одна ошибка или более дб ошибок \ Конец Рис. 1.9. Алгоритм исправления двух ошибок 30 Начало Определение лонатород 1, Устаповка начально ед 3ha4ctWR перемен  Нет Нет Определение Вычисление ошибон £i и Sj. 1 коррекция ошиВок Более двух ошибок Вычисление  Конец J Рис. 1.10. Алгоритм локализации и коррекции двух ошибок чиспение meKyatetg значении перееденной.  Вычисление Вычисление локаторов Пет  Вычисление ошибок £/ и fi; Вплее двух ошидок Коррекция ошибок Ноиец) Рис. 1.11. Алгоритм определения корней квадратного уравнения при исправлении двух ошибок табличным методом Таблица 12. Системы уравнений синдромов Синдром ошибок Модифицированный синдром Si = Xl 8р s3 = x\ Ер 50 = Bpi + 51 = Xl Spi + 8p sj = a:? 8c.. -f- x2 *2 Oj s3 X Sp + xl 8q 50 = 1 So + Si 51 = XiSi + S, 52 + X1 Sj + Ss So = Sfi + Bp2 Si = Xl Вру + X2 Zp2 Sa = 3? ej -- Bp2 So - 8/7] + 8/72 + Oj Si = a:j e + Xi Sp2 + Sa = x\ 8p + x\ Bp2 + xl Bq Sb = x] Bpi + xl Sp2 + 4 80 50 = ATg So + Si 51 = 2 Si + So = Bpi + 8/72 + 8/73 51 = a:i 8/71 + 2 6/72 + 3 e/?3 52 - xl 8/7] + 2 8/72 ~b s4 = xf 8/71 + 2 + - з F3 So = л^з So + S( 50 - 8/7] 6/70 -j- 8/73 -j- 8/7 51 = XiBpi-\- X2 Bp2 + Jt3 8/73 + 6/74 Sa = д| 8/7] l Л; 8/72 Ь 3 ®F3 ч 4 s3 = 8/7, 8/72 83 + *4 Локатор ошибки Ei = So Критерий идентификации So = Si = = 0 Хг = а' Sq Si ei = So + Ea So, Si.Sa ?i 0 Л'=5+ SiSa = < m = 2 Se = Si = Ot .-A ДГ3 - , = (so + - (Xi + Хз) (Xa + X3) Л^а + ЛГз / 1 - So -- 63 -f- ба m = 2 So, Si?£0 m = 3 So = 0 84 = So [(*i + (Xa + Xi) (X3 + Xi)] ei=So+ea + e3-f 84 m = 4 So 50 Бели в блоке одно стирание и одна ошибка (ел- и ео), то возможны два расчетных соотношения для локатора ошибки, в которые входят модифицированные синдромы So, Si и Зг. J2 = a = 5i/5o. (1,22) Из этих равенств следует основной критерий идентификации So, Si, SaO. (1.23)  Лона/газации одной ошибка локализация двух ouiuSoH Коррекция одного стирания Локализация одной, ошибки Коррекция двух стираний Локализация одной ошибки Коррекция трех стираний Коррекция четырех стираний Конец J Рис, 1,12. Алгоритм исправления ошибок и стираний 34 1 2 3 4 5 6 ... 22 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||