
 | |
 |
Главная » Мануалы 1 2 3 4 5 6 7 ... 22 Из (1.23) может быть получен и дополнительный критерий который определяет наличие одной ошибки и одного стирания в блоке: Л'=5? + 5 о5; = 0. Используя модифицированные синдромы, можно получить расчетные формулы для двух ошибок, когда одна из них стерта- Ч~ S(,/{Xi-\-х^), ei = 5Q + 82. Если в блоке три ошибки, из которых две стерты, то в расчетах участвуют еще два модифицированных синдрома, связанных следующими равенствами с ранее введенными модифицированными синдромами: Sq- X2SQ-f-5j, Si - 2 Si 4 52. При этом локатор ошибки Xg = Si/Sq. Из этой формулы следует, что критерием одной ошибки и двух стираний является выполнение неравенства SoU5iO. С использованием модифицированных синдромов расчетные формулы для ошибок и стираний имеют простой вид: 4 = Sf,/{Xi + Xs)ix + X3); 82 = [So + Si/(x + X,)] (Xi + 2)-; 81 = So-f 82 4-83. Эти расчетные формулы справедливы и для трех стираний, тогда $0=0. В случае четырех стираний удобно использовать модифицированный синдром 0 ~ XgSo-\- Si. Тогда 8, = So liXi + Xi) (Хз + Xi) (Хз + Xi)r , 83 = [So + So/ixs + Xi)] lix, + X,) (Xi + Хз)]- , 82 = [So + 83 {Xi + Xs) + 8, (Xi + Xi)] {Xi + ЛГа)- , 81 = 50 + 82 + 83+84. Для пояснения изложенного материала на рис. 1.12 приведен алгоритм исправления ошибок <и стираний в одной ступени декодирования кода CIRC, который обеспечивает реализацию потении-[ьных возможностей кода по исправлению ошибок. Стратегии декодирования кода CIRC. Стратегии декодирования кода CIRC различаются по следующим признакам [9, 12]: по числу исправляемых ошибок в первой и второй ступенях декодирования, по числу исправляемых стираний в первой и второй ступенях декодирования и по использованию стираний для уменьшения вероятности неправильной идентификации ошибок. В настоящее время декодер кода CIRC реализуется в виде специализированного вычислительного устройства, имеющего ОЗУ и процессор, где алгоритм работы обеих ступеней декодирования задается программой. В зависимости от стратегии декодирования в этом устройстве имеются блоки, яроизводящие вычисления одиночных, двойных ошибок и стертых символов. Поэтому, если хотя бы в одной ступени исправляются две ошибки, то такое же число ошибок может быть исправлено и в другой без усложнения и переделки декодера. Из этого следует, что из многих возможных вариантов исправления ошибок практический интерес представляют лишь два: исправление одиночных или двойных ошибок, существенно отличающихся исправляющей способностью, и сложность реализации. Обязательно используются стирания при отказе декодера от исправления ошибок для обеспечения возможности интерполяции этих ошибок при декодировании кода CIRC. Использование стираний позволяет повысить исправляющую способность декодера и уменьшить вероятность неправильной идентификации и, как следствие, ложного исправления и размножения ошибок. Стирания могут вводиться в декодере EFM в первой и второй ступенях декодирования, причем они могут быть различного уровня и индицироваться различными флагами с тем, чтобы отличить стирания, введенные в различных местах и при разных условиях. Все это создает большие возможности для поиска оптимальных стратегий декодирования кода CIRC в зависимости от статистических характеристик кодовых ошибок и в особенности от характера пакетов ошибок. Особый интерес представляют две стратегии декодирования: регулярная стратегия декодирования с исправлением двойных ошибок и суперстратегия декодирования фирмы Sony, которая наиболее широко используется в проигрывателях компакт-дисков. Регулярная стратегия записывается: а) для первой ступени декодирования {Д1) г=0, исправления ошибок нет, г=\, Г-2 - исправление ошибок, г>2 - введение флагов стираний Fl; б) для второй ступени декодирования г=0 - исправления ошибок нет, исключение флагов Fl; г=1, т = 2--исправление ошибок, исключение флагов Fl, />2, т^З - исправления ошибок нет, флаги F1 подтверждаются (копируются), г>2, 2т^2 - исправления ошибок нет, вводятся флаги стирания F2. Расчет исправляющей способности любой стратегии декодирования наиболее просто выполняется в предположении, что ошибки на входах обеих ступеней декодирования кода CIRC случайны и независимы. Такое допущение достаточно правомочно, так как при деперемежении кодовых символов осуществляется декорре-ляция ошибок. Вероятность ошибочных блоков на выходе первой ступени декодирования может быть представлена в виде суммы двух членов Рб.вых 1 2 (Овх 1 где г - число ошибочных символов в блоке; ti - число ошибок, исправляемых в Д1; т - длина блока (ni=32). Первый член в этой формуле определяет вероятность правильно идентифицированных, но неисправленных блоков, так как число ошибок в них превышает исправляющие возможности ступени. Эту вероятность обозначим Р'б.вых! (?). Второй член формулы определяет вероятность неправильно идентифицированных и, следовательно, ложно исправленных блоков. Эту вероятность обозначим Р б.вых1 (г). Для случайных независимых ошибок вероятность ошибочных блоков на входе Д1 подчиняется биномиальному закону распределения Рб{г..)=С:,РАо)Рое о'-, где Рс(ео) и Рс{ео) - вероятности соответственно ошибочных и безошибочных символов, сумма которых равна 1. В формуле (1.24) oWi= 1-61. где Peir)! - безусловная вероятность неправильной идентифика. ции, определяемая общим равенством oWiii 2 Рб(г, 0), /. л. (1.25) 1=0 и=</ Условная вероятность неправильной идентификации Рб(г, а, I, n)i определяет вероятность того, что блок с г ошибками идентифицирован как блок с / ошибками и в результате ложного исправления в нем стало а ошибок (со>г): Рб(г, со, /, ), = (-1)- Л (0) 2 C-?C;{q-\Y-{q-2), (1.26) с = / -г -co-f 2р, Где Л (со) -весовой спектр кода RC в поле из (1.5): со- вес кодового блока; d - кодовое расстояние. В рассматриваемой стратегии декодирования ошибочные и безошибочные символы на выходе Д1 могут быть без флагов и с флагами (стертые), вероятности которых обозначаются: Pc(eo)i, Pc(8p)i, Pc(eo)i и Pc(ep)i. Их расчет производится через Р'б()вых1 и Р б()вых1 путем умножения каждого члена ряда на число оши. бочных (безошибочных) символов в блоке с нормированием всей суммы на длину блока Poi%)i = b S 2 2 б( )вxlб( /. 1)1. PciF)=n-i 2 oMbxioWi, (1.27) PcMi = r* 2 (ni--)6(-)Bxi6(-i). Ha основе этих вероятностей ошибочных символов могут быть рассчитаны вероятности ошибочных блоков на выходе Д2 б.ВЫХ2= S Рб(-)вХ2б(-)2+ 2 б(-)вХ2б(-)2. (1.28) где = 1-6 ()2. Л5 {г)2 = 2 Е ( /. 2)2. 1=0 (o=d а Рб(, со, /, 2)2 рассчитывается по формуле (1.10) при 2=28. Учитывая, что на входе Д2 вероятность ошибочных символов Pe(8)i = P,(eo)i + Pc(eF)i, (1.29> а вероятность безошибочных символов c(e)i=Pc(6o)i + nMi. (1-30> при возведении этих выражений в степень можно использовать разложение в биномиальный ряд. Расчетное выражение для Рб{г)ъх2 может быть преобразовано к виду г п^-г 6Wbx2= Е Е Р^{Г, h Овх2. (1.31> /=0 1=0 где Рб {г, и Овх 2 = Сп, dr С.-Г Ро Ы{ Рс ЫГ Рс (6f)i Рс (бо) (У, i - числа символов в блоке вида bf и вр). На выходе декодера прежде всего представляет интерес вероятность ошибочных символов Рс(8о)2. которыб не обнаружены и, следовательно, не могут быть исправлены даже частично. При воспроизведении звукозаписи такие ошибки проявляются в виде щелчков, резко ухудшающих качество восприятия музыкальной программы. Ошибочные символы, которые обнаружены, но не исправлены, могут быть помечены флагами стираний и затем частично исправлены с помощью линейной интерполяции. Стирание неисправленных ошибочных символов неизбежно сопровождается 38 стиранием и безошибочных символов, которые также интерполируются. Поэтому общая вероятность интерполирования символов равна Расчет этих вероятностей существенно зависит от условий использования стираний в Д1 к Д2. Для рассматриваемой стратегии декодирования расчетные формулы имеют вид л(f)2 = - 2 2 2 (/ + о( /> Овх.РЛг)г, (1.32) r=t,+ l 1=0 1=0 Рс (80)2 = 2~ 2 2 2 - /) б (-. /, Овх 2 б {rh + r=t,+l 1=0 I =0 2 2 2 2 2 Pr, j, 1)вх2Рб(-. t, 2)2-r=/,+i /=0 г=о 1=0 w=d Для приближенных расчетов можно пользоваться более простыми формулами, которые получаются при ограничении сумм только наиболее вероятными членами рядов: Po(f)2 = 3,53-10 Ре(8) , Ре (80)2 = 2,71.10 Po(e)g. (1.33) В данной стратегии при Рс(8)о=10з вероятность необнаруженных ошибочных символов на выходе понижается до 2,6 10~*, а вероятность символов, которые интерполируются, равна 4,2X X 10-17. Общая задача оптимизации стратегий декодирования состоит в том, чтобы существенно уменьшить вероятность необнаруженных ошибочных символов без заметного увеличения вероятности интерполированных символов. Эта задача решается оптимальным выбором условий введения стираний в Д1 и Д2, а также использованием стираний для уменьшения вероятности неправильной идентификации, особенно при исправлении двойных ошибок, когда эта вероятность достаточно велика и равна 4,6-10-. Вероятность Рс(8о)2 можно существенно уменьшить, если при исправлении двойных ошибок в Д1 ввести стирания, а в Д2 исправить двойные ошибки только при условии совпадения локаторов ошибок с локаторами стираний. Эти две особенности и являются основными отличительными признаками суперстратегии декодирования. Для формальной записи этой стратегии декодирования обозначим число совпадаемых локаторов Я. Оно может быть равно 2, 1 и О, тогда: а) для первой ступени декодирования (Д1) г = 0- исправления ошибок нет, г=1 - исправление одной ошибки, г = 2 - исправление двух ошибок, введение стираний FI, />2 - исправления ошибок нет, введение стираний FI; б) для второй ступени декодирования (Д2) r=0 - исправления ошибок нет, исключение флагов f1, г=1 - исправление одной ошибки, исключение флагов Fl, г=2, Я=2, т>4 -копирование флагов Fl, т^4-исправление двух ошибок, исключение флагов Fl, Я=1, f>3 - копирование флагов f1, /3 - введение стира* ний f2, Я=0, />2 - копирование флагов Fl, /2 - введение стираний f2. На рис. 1.13, 1.14 приведены алгоритмы суперстратегии, а на рис. 1.15 представлены результаты расчетов исправляющей способности. В отличие от регулярной стратегии декодирования здесь вероятность необнаруженных ошибочных символов Рс(ео)2 меньше на 3... 12 порядков в зависимости от значения Рс{е)о- При этом вероятность интерполяции заметно возрастает лишь при очень малых вероятностях ошибочных символов на входе. При-
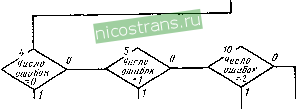
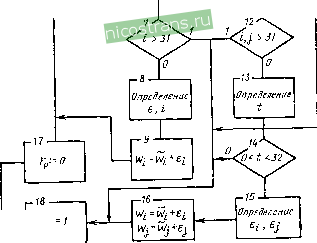 Рис. 1.13. Первая ступень алгоритма суперстратегии декодирования 40
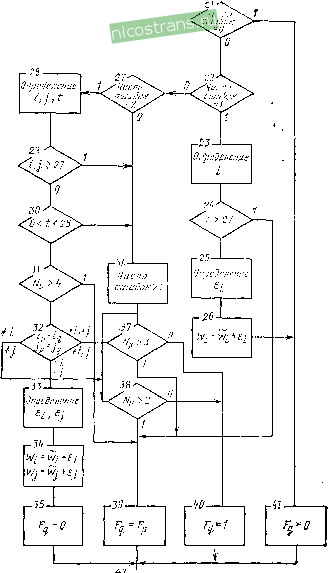 Фис. 1.14. Вторая ступень декодирования алгоритма суперстратегии веденные кривые хорошо аппроксимируются линейными функциями Ре(/) = 3,53.10 Ре(в)? и Ре (80)2 = 8,93.10 Ре (8)2. В суперстратегии декодирования фирмы Sony исправление-стираний не производится, поэтому потенциальные возможности кода CIRC реализуются далеко не полностью. Использование стираний для проверки локаторов ошибок позволило только-уменьшить вероятность ложных исправлений двойных ошибок в. обеих ступенях декодирования и этим частично исключить эффект размножения ошибок при неправильной идентификации. Одновременное исправление ошибок и стираний требует существенного повышения быстродействия, емкости памяти и сложности декодера. Исправление выпадений и пакетов ошибок в коде CIRC. Исправление следует разделять на полное и частичное. Полное исправление обеспечивается, если благодаря деперемежению пакет ошибок в первой и второй ступенях декодирования преобразуется-в ошибки и стирания, число которых не превышает исправляющей возможности декодера. Частичное исправление выпадений: и пакетов ошибок с помощью линейной интерполяции выполняется при условии, что в каждом звуковом канале имеются только-одиночные ошибочные слова со стертыми символами. Короткое выпадение исправляется в Д1, если после депереме-жения число ошибочных символов в блоке не превышает исправляющей способности этой ступени (две ошибки, три или четыре стирания). Так как длина одного деперемещения всего один блок, то в первой ступени может быть исправлено выпадение длиной от двух до восьми символов. Для этого необходимо, чтобы в следующих блоках не было ошибок. Это значит, что защитный интервал должен быть не меньше двух блоков. Длина полностью исправляемого длинного выпадения определяется принятой в коде CIRC системой деперемеже-ния символов и исправляющей способностью второй ступени декодирования. Эта зависимость иллюстрируется рис. 1.16, где Ыб - длина выпаде- 10 p,kk
Рис. 1.15. Вероятность ошибочных Pc(8o)2 и интерполированных PcU) символов на выходе декодера CIRC: 1 - при суперстратегии декодирования, г - при регулярной стратегии декодирования 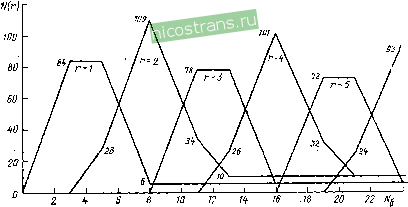 Рис. 1.16. Зависимость числа блоков с г ошибочными символами на входе 2-й ступени кодирования от длины выпадений Nn (в блоках) на входе декодера CIRC НИЯ в блоках, а N(r) - числе блоков с г ошибками на входе Д2. Если в Д2 исправляются только одиночные ошибки, те полностью исправляются выпадения длиной до трех блоков, если одиночные и двойные - то восемь блоков. При дополнительном исправлении трех и четырех стираний длина полностью исправляемых выпадений увеличивается до 11 и 16 блоков соответственно. В случае длинных выпадений в Д1 производится только стирание всех символов в блоках, которые после деперемежения распределяются в пределах зоны, равной 109-}-ЛГб блоков, и на входе Д2 формируется достаточно длинный пакет ошибочных блоков, в котором преобладают блоки с г и (у+1) ошибками. Чем больше ЛГб, тем больше г и меньше вероятность исправления. Полное исправление таких выпадений возможно лишь при условии, что зоны перемежения двух последовательных выпадений не пересекаются. Это значит что защитный интервал должен быть не меньше зоны перемежения, и что длинные выпадения могут быть исправлены тогда, когда они относительно редки. С увеличением длины выпадений выше исправляющей возможности декодера сначала увеличивается число одиночных ошибочных слов в звуковых каналах, которые могут быть исправлены с помощью линейной интерполяции. Затем начинают появляться подряд ошибочные слова по два, три и больше, которые могут быть исправлены лишь с использованием интерполяции нулевого порядка (удержание) или цифровой фильтрации высокого порядка. Эта зависимость иллюстрируется рис. 1.17,а и б. Из рисунка видно, что пока iVSl блока, на выходе декодера могут быть лишь одиночные ошибочные слова (а=1). Число этих слов и, следовательно, вероятность интерполяции существенно зависят 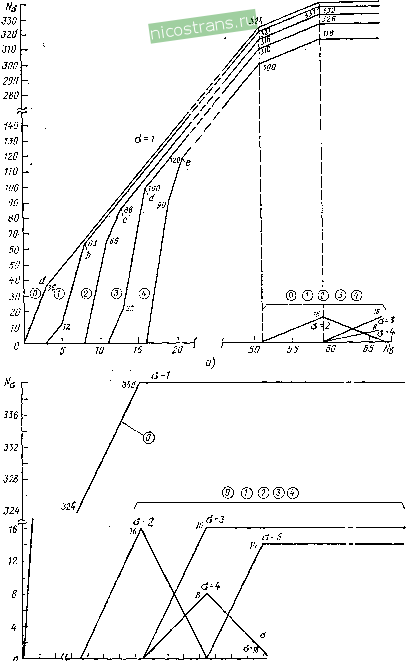 W 2S M SZ 6f m M rs гг л /s ss as m ret XXXXXXXXxX xxxxxx J 1 I Ui I I ~ Z * W SZ 5i SS 58 SO S2 Si- SS 6i 70 7Z Tt 76 78 80 8Z 36 38 1 2 3 4 5 6 7 ... 22 |