
 | |
 |
Главная » Мануалы 1 2 3 4 ... 18 Создание термоэлектродных сплавов связано в немалой степени с основной задачей улучшения использования топливно-энергетических ресурсов, поставленной перед промышленностью директивными органами и зафиксированной в Основных направлениях экономического и социального развития СССР на 1981-1985 годы и на период до 1990 года . В немногочисленной литературе по сплавам с особыми физическими свойствами термоэлектродные сплавы занимают незначительный объем: в отечественной, да и в мировой литературе найдется всего лишь несколько книжных публикаций по указанному вопросу. Обычно сплавы для термопар описываются только в соответствующих разделах книг по термометрии, физическим свойствам металлов или монографий, посвященных сплавам каких-либо определенных металлов. Авторы попытались восполнить указанный пробел в предлагаемом справочно.м руководстве по свойствам промышленных сплавов для термопар. В вводных главах руководства даны необходимые общие сведения о термоэлектрических явлениях и механизмах т.э.д.с. в металлах и сплавах. Основное содержание руководства - свойства промышленных термоэлектродных сплавов, изготавливаемых, применяемых и стандартизированных в СССР и странах СЭВ. Наиболее подробно представлены метрологические характеристики: температурные зависимости т. э. д. с. и чувствительности, градуировочные таблицы, сведения о рабочих атмосферах, сроках службы и дрейфе показаний термопар. Важнейшим свойствам термоэлектродных сплавов - однородности и стабильности т. э. д. с. - посвящены специальные главы, в которых наряду с обширным фактическим материалом анализируются металлургические факторы и процессы, влияющие на эти свойства, В заключительных главах рассматривается влияние экстремальных условий эксплуатации термопар: радиации, высокого давления, сильных магнитных и электрических полей, на термоэлектрические характеристики термоэлектродных сплавов, В справочном руководстве обобщены литературные данные о свойствах термоэлектродпых сплавов, опубликованные по 1980 г. включительно. В данную книгу не вошли сведения о неметаллических термоэлектродных материалах, о некоторых сплавах для термопар, имеющих более узкое применение, пленочных термопарах и др. и в небольшом объеме представлены данные о неметрологических характеристиках сплавов, в частности о механических и физических свойствах. Вне поля зрения остались вопросы технологии производства и ряд особенностей эксплуатации термоэлектродных сплавов. ВВЕДЕНИЕ Температура - один пз важнейших контролируемых параметров технологических процессов практически во всех отраслях народного хозяйства. Известно, что около 40 % всех измерений в промышленности п научных исследованиях составляют измерения температуры. Не менее 60 /о всех температурных измерений приходится на долю термоэлектрических термометров или, как их часто называют, термопар. Область температур, измеряемых термопарами, охватывает диапазон от 0,5 до 3000 К. Широкому применению в промышленности и научных исследованиях термопары обязаны в первую очередь своей простоте, удобству монтажа, возможности измерения температуры в труднодоступных участках и локальной температуры. К числу достоинств термопар относятся также широкий диапазон измеряемых температур, малая инерционность, возможность измерения температуры поверхности, температуры быстротекущих процессов, малых разностей температур и т. п. Термопары могут обеспечивать высокую точность (в некоторых случаях до 0,01 К) и высокую чувствительность (до 80-100 мкВ/К). Все осиовные параметры термоэлектрических термометров определяются свойствами чувствительных элементов, которые в свою очередь определяются свойствами термоэлектродиых сплавов, из которых они изготовлены. Одной из основных характеристик термоэлектродных сплавов является стабильность этих свойств при эксплуатации термопар при высоких и низких температурах в различных средах и при различных внешних воздействиях; механических, электрических и др. Очень большое значение имеют технологичность, а также однородность и воспроизводимость термодинамических свойств в условиях промышленного производства термоэлектродиых сплавов и изготовлеипя из них термопар. В качестве термоэлектродных материалов применяют самые разнообразные цветные, благородные и тугоплавкие металлы и сплавы. Широкое использование переходных металлов и сплавов на их основе обусловлено сравнительно высокой т. э. д. с. В области криогенных температур в последнее время используются сплавы непереходных металлов с ферромагнитными легирующими элементами, также развивающие большую т. э. д. с. Большое число зачастую противоречивых требований к термоэлектродным сплавам весьма усложняет создание необходимых материалов. В ряде случаев условия эксплуатации термопар или требования гарантированной точности измерений вынуждают использовать, например, сплавы с невысокой чувствительностью, но работоспособные в определенных температурных и иных условиях с приемлемой стабильностью. В будущем разработка новых термоэлектродных сплавов, вероятно, окажется целесообразной лишь в отдельных специальных случаях, например для работы в каких-либо экстремальных условиях, в которых известные сплавы применимы быть не могут. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ. ТЕРМОЭЛЕКТРИЧЕСКИЙ ТЕРМОМЕТР 1.1 ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ Термоэлектрическими называются явления, обусловленные связью между тепловыми и электрическими токами. К настоящему времени сформулированы микроскопическая (или кинетическая) теория термоэлектричества, связывающая наблюдаемые термоэлектрические свойства с характеристиками энергетических спектров и процессов рассеяния носителей тока в твердых телах, и термодинамическая теория, объясняющая макроскопические закономерности термоэлектрических явлений и связь между различными термоэлектрическими эффектами. В тер.модинамической теории используются линейные соотношения между потоками и обобщенными силами , вызывающими эти потоки. Частными случаями таких соотношений являются закон Ома, устанавливающий пропорциональность между электрическим током (потоком) в изотермическом проводнике и электрическим полем (градиентом электрического потенциала), и закон Фурье, устанавливающий пропорциональность между тепловым потоком в отсутствие электрического тока и градиентом температуры. Коэффициентами пропорциональности в этих законах являются соответственно изотермическая проводимость и коэффициент теплопроводности в отсутствие электрического тока. В более общем случае, когда в проводнике одновременно присутствуют градиенты температуры vr и электрического потенциала VV (обобщенные силы), возникают оба потока - заряда / и тепла Q, линейные соотношения между силами и потоками приобретают вид: I = hiy + LnVT\ (1.1) Q = L2ivV-i-L22V7. (1.2) где L - коэффициенты. Соотношения (1.1) и (1.2) позволяют в принципе предсказать существование трех термоэлектрических эффектов: Зеебека, Пельтье и Томсона, установленных экспериментально. Эффект Зеебека. В замкнутой цепи, состоящей из двух разнородных металлических проводников Л и S (рис. 1.1, а), температура соединений спаев которых поддерживается различной, появляется электрический ток. Электродвижущая сила или равная ей разность потенциалов на концах разомкнутой цепи, состоящей из двух разнородных металлов, когда температуры спаев различны 1 Согласно соотношению (1.1) в однородном проводнике в отсутствие электрического тока возникает электрическое поле или градиент потенциала VV=- rVT, а на концах этого проводника разность потенциалов AV (т. э. д. с); ДУ = - уТ (х) dx = -\ ks/T{x)dx, (1.3) где k=L,2JLn в общем случае - функция температуры; дс -координата по длине проводника. называется термоэлектродвижущей силой или сокращенно т. э. д. с. (интегральной т.э.д.с.) пары АВ и обозначается Еаб (рис. 1.1,6). Эта цепь называется термоэлементом или (в термометрии) термопарой. Для бесконечно малой разности температур спаев dT т. э. д. с. dEAB = eABdT, где елв - дифференциальная т.э.д.с. пары АВ*. 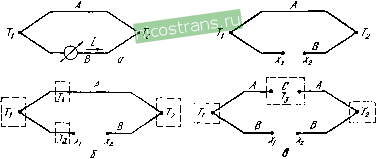  /( измеритемнам приЛру Рис. 1.1. Термоэлектрические цепи и законы термоэлектричества: а - термоэлектрический ток / в замкнутом контуре и термоэлектрическая разность потенциалов V в разомкнутом контуре; б - к закону однородной цепн х,х,.~ АВ в -к закону промежуточных металлов V tT Т\---------- .......Ji-v., ouxvvynj х,х2~ АВ ~ закону промежуточных металлов 2 (Л, г -схема измерения температуры термопарой Эффект Пельтье. Если через область контакта двух разнородных проводников течет электрический ток /, то в этой области выделяется или поглощается в единицу времени некоторое количество тепла Qn определяемое выражением: (1.4) где П - коэффициент Пельтье. В отличие от джоулева тепла, пропорционального квадрату силы тока и всегда выделяющегося в проводнике, теплота Пельтье носит обратимый характер, т. е. может выделяться или поглощаться в зависимости от направления тока. Эффект Томсона представляет собой поглощение или выделение тепла в однородном проводнике, в котором течет ток / и * Величину Вав (скорость изменения Еав в зависимости от температуры) называют также температурным коэффициентом т. э. д. с, коэффициентом Зеебека, чувствительностью или дифференциальной т. э. д. с. термопары. вдоль которого существует градиент температуры VT. Теплота Томсона (в единицу времени) определяется выражением: (1.5) где 0 - коэффициент Томсона. В замкнутой цепи, по которой протекает электрический ток, при наличии градиента температуры возникают все три термоэлектрических эффекта, связь между которыми определяется соотношениями Кельвина: a = TdSldT\ n = rS, (1.6) где S - абсолютная дифференциальная т. э. д. с. В связи с тем что температуру термопарами обычно измеряют в отсутствие тока, основным эффектом, существенным для понимания работы термопар, является эффект Зеебека, два других эффекта в данном случае значения ие имеют. Многочисленные экспериментальные исследования свойств термоэлектрических цепей позволили сформулировать следующие три эмпирических закона. Закон однородной цепи (закон Магнуса). В замкнутой цепи, состоящей из однородного проводника, электрический ток не может поддерживаться за счет перепадов температуры: ЛлГг. 7i) = 0. (1.7) Следствием этого закона является тот факт, что в цепи, состоящей из двух разнородных проводников, спаи между которыми поддерживаются при двух различных температурах Г, и Тг, т.э.д.с не зависит от распределения температуры вдоль проводников, а лишь от температур спаев (см. рис. 1.1,6). Закон промежуточных металлов. Основная формулировка этого закона: алгебраическая сумма т. э. д. с. в цепи, состоящей из любого числа различных металлов, равна нулю, если вся цепь находится при одной температуре: лсГх. Т,) = Е^{Т^, Г^) + £всГ1. Т,) = 0, (1.8) В этой формулировке закон аналогичен второму началу термодинамики, так как наличие не равной нулю т.э.д.с. привело бы к появлению тока, что в свою очередь вызвало бы охлаждение одних частей цепи и нагрев других. Это означало бы, что должен происходить перенос тепла от участков с более низкой температурой к участкам с более высокой температурой в отсутствие внешнего источника энергии, что противоречит второму началу термодинамики. Из закона следует, что при введении в контур, содержащий два разнородных проводника Л и В с температурами спаев Ti и Гг, третьего проводника С, находящегося при одинаковой по всей его длине температуре Гз, т.э.д.с. £ab(7 i, Ti) не меняется (рис. 1.1, в). Эквивалентная формулировка закона промежуточных металлов: т. э. д. с, возникающая в цепи из двух различных проводников АВ, равна алгебраической сумме т. 9. д. с. цепей, образованных третьим проводником С и проводниками А и В: (1.9) Закон последовательных, или промежуточных температур. Т.э.д.с цепи, состоящей из двух различных однородных проводников Л и В, спаи которых имеют температуры Г, и Г равна алгебраической сумме т.э.д.с. той же цепи при температурах спаев ЛвГз- 71) = ИвГз. 2) + ЛвГ2> Т,). (1.10) Все три закона можно объединить и сформулировать следующим образом: т.э.д.с. цепи, состав.ченной из нескольких различных однородных проводников, является функцией только температуры спаев и не зависит от градиентов температуры вдоль проводников. На основе этих законов осуществляется практическое использование термоэлектричества в термометрии (см. раздел 1.2). С законом однородной цепи связано применение наиболее распространенной схемы измерения температуры термопарами, при которой один из спаев ( свободные концы ) поддерживается при постоянной температуре, а другой спай находится при измеряемой температуре (рис. 1.1, г). При этом величина сигнала является только функцией измеряемой температуры. Используя закон промежуточных температур, можно вносить поправки на температуру свободных концов и градуировать термопары. Основываясь на законе промежуточных металлов, можно вводить в цепь термопар измерительный прибор, а также при необходимости конструкционные или токоведущие элементы или объект, температура которого измеряется, при условии их изотермичности. При этом результирующая т. э. д. с. сохраняется неизменной. Этот же закон служит основанием использования так называемых удлиняющих проводов. Тэ. д. с. термопар является сложной функцией температуры, но для многих пар металлов в диапазоне температур в несколько сотен градусов ее величину можно аппроксимировать с приемлемой точностью полиномом второй степени. Из термодинамического рассмотрения термоэлектрических эффектов следует, что т.э.д.с. пары АВ равна алгебраической сумме т. э. д. с, возникающих в каждой из ветвей, т. е. для пары однородных проводников: (T)dT= \SdT- SdT, (1.11) Величины Sa и Sb представ.чяют собой абсолютную (дифференциальную) т. э. д. с. материалов Л и В, т. е. разность потенциалов, возникающую на концах проводников А и В, помещенных в температурное поле с единичным градиентом. Эти величины являются характеристикой данного материала подобно, например, удельному электросопротивлению или коэффициенту теплопроводности и зависят от температуры, состава и состояния материала. Дифференциальная т. э. д. с. термопары представляет собой разность абсолютных (дифференциальных) т. э. д. с. каждой из ветвей: (1.12) В реальных условиях т.э.д.с. всегда измеряется в цепи, состоящей, как минимум, из двух материалов - термоэлектродного и материала соединительных проводов. В связи с этим в технической литературе иногда высказывается ошибочное мнение о том, что т.-э. д. с. подобно теплоте Пельтье возникает в области спая двух металлов. Между тем для появления т. э. д. с. не требуется двух металлов, поско.чьку она возникает в однородном проводнике в области градиента температуры см. уравнения (1.3) и (1.11). Электрическая разность потенциалов AV, возникающая на концах однородного проводника, вдоль которого создается перепад температуры ДГ, включает, помимо т.э.д.с, SAT (т. е. свойства переноса) и изменение химического потенциала i носителей тока (т. е. статическую характеристику): -1дГ. (1.13а) AV = Аналогично для термопары, состоящей из двух электродов Л и В, разность потенциалов на концах этихэлектродов: {\A-в)+SA-Sв (1.136) В реальных условиях при наличии соединительных проводов, подключенных к концам проводника нли к свободным концам термопары, из условия непрерывности электрохимических потенциалов в точках соединений (электрический и химический потенциалы имеют в этих точках скачки) следует, что измеряемая в отсутствие тока разность потенциалов между концами этих проводов равна: в случае одного проводника X Axt = (Sx-Sz.)Ar, (1.14а) в случае термопары с электродами А и В Vab = {Sa-Sb)T, (1.146) где индексы А, В, X и L относятся к электродам и соединительным проводам. Таким образом, измеряемая разность потенциалов на концах термопары определяется только величиной т.э.д.с. и не включает скачков химического потенциала в местах соединений (спаев). Абсолютную т. э. д. с. можно найти косвенным путем по температурной зависимости теплоты Томсона, измеренной калориметрически, с помощью соотношения: Т S=\(alT)dT. (1.15) о Абсолютная т. э. д. с. металлов и сплавов вычисляется пз соотношения (1.12) на основании результатов измерения дифференциальной т. э. д. с. относительно эталона Сравнения, значения абсолютной т.э.д.с. которого известны. В качестве эталона используют обычно платину, медь, золото, вольфрам (для температур >100К) и свинец (для температур 10-350 К). В области, низких температур (<20К) абсолютную т.э.д.с. определяют по результатам непосредственных измерений относительно сверхпроводников, т. э. д. с которых при температурах сверхпроводящего перехода исчезающс мала. Значения абсолютной т. э. д. с. большинства металлов н сплавов колеблются в пределах (0-80) мкВ/К. При учете концепции абсолютной т. э. д. с. становится очевидным определение знака т.э.д.с. Т.э.д.с пары АВ положительна, если Sa>Sb- для клаееичеекой схемы термопары (см. рис 1.1 г) материал с более высокой положительной т.э.д.с. (Л) имеет более высокий потенциал на свободном конце в точке xj, если температура свободных концов Го<Г. В общем случае термоэлектрическая разность потенциалов на зажимах контура, включающего пару неоднородных термоэлектродов, равна: ав = § Т) vr (x) dx = § [S{x, Т) - -Ss{x,T)]yTdx, 1.16) откуда для однородных электродов получается известное соотношение: ав= \ (5л-5£)у7йх = I (5д-5в)ЙГ. (1.17) Tl Tt Из выражения (1.16) следует важный с практической точки зрения результат: части термоэлектрических цепей, находящиеся в изотермических условиях, ие дают вклада в наблюдаемую т. э. д. с. 1.2. ТЕРМОЭЛЕКТРИЧЕСКИЙ ТЕРМ0Л1ЕТР Измерение температуры, оенованнос па иенользовапин одного из термоэлектрических явлений (эффект Зеебека), осуществляется с помощью термоэлектрических термометров. Чувствительным элементом термоэлектричсекого термометра служит термопара, а термометрическим свойством является т. э. д. е., возникающая в термопа- 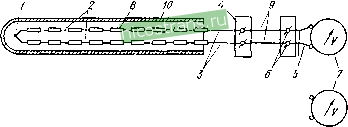 Рис. 1.2. Схема термоэлектрического термометра: / - рабочий спай; г - термоэлектроды; 3 - свободные концы; -промежуточный спаи; 5 - медные провода; 5 - реперные спаи; / - измерительный прибор; 8 - изоляция; 9 - удлиняющие (компенсационные) провода; 10 - защита ре. Комплект термоэлектрического термометра (рис. 1.2) состоит из термоэлектрического преобразователя, основой которого является термопара, и вторичного прибора (обычпо потенциометра, реже милливольтметра). В подавляющем большинстве случаев термопара состоит из двух термоэлектродов (электродов), соединенных в ра- бочем спае*. Если свободные концы термопары находятся при постоянной температуре, то соединяющие провода выполняются из электропроводного и дешевого материала (меди) (рис. 1.2). Если же температуру свободных концов термопары невозможно поддержать постоянной, то соединяющие термопару и вторичный прибор провода выполняют из материалов, которые в области температур свободных концов термопары имеют практически те же термоэлектрические характеристики, что и материалы термоэлсктродов. Эти провода называются удлиняющими или компенеационными (другие названия: удлинительные, термоэлектродные). Удлиняющие провода служат для удлинения термопары и переноса ее свободных концов в зону постоянной (мало меняющейся) температуры. В случае, когда температура промежуточных спаев одинакова, пользуются проводами, которые в паре имеют такую же температурную зави-спмоеть т.э.д.с, что и термопара (так называемые провода с суммарной компенсацией). В том случае, когда температура промежуточных спаев различна, употребляют провода, каждый из которых обладает такой же температурной завиеимоетью т.э.д.с, что и соответствующий термоэлектрод термопары (так называемые провода с поэлектродной компенеацией). Точное измерение температуры с помощью термоэлектрического термометра возможно при условии, если известна температура сво-   Темпвратура Температура Рнс. 1.3. Градуировочные кривые термопар: а -обычная термопара; б -термопара, не требующая термостатн-ровання свободных концов и поправок на нх температуру бодных концов. Знание последней позволяет внести поправки на изменение температуры репериого спая по сравнению с той, при которой была произведена градуировка термометра. Использование удлиняющих проводов не избавляет от необходимости введения поправок на температуру репериого спая, поэтому большинство Рабочий спай называют также измерительным или горячим (при измерении температур выше 0°С). 2 Свободные концы, находящиеся при известной (лучше постоянной) температуре, называют реперным или опорным епаем; при использовании удлиняющих проводов свободные концы называют также промежуточным спаем. Большинство авторов считают термины свободные концы и реперный спай синонимами. промышленных термометров снабжено автоматическим устройством для введения таких поправок. Существуют термонары, не требующие поправок на температуру репериых спаев, в которых используются термоэлектродные сплавы, развивающие в паре т. э. д. с, не зависящую от температуры свободных концов в широкой области температур (рис. 1.3). Термоэлектрические явления и их основные закономерности, термоэлектрические термометры (термопары) и практика измерения ими температуры рассмотрены во многих монографиях (например, [1, 7, 10-11, 21, 22]) и в соответствующих разделах руководств и трудов конференций по термометрии (например, [2-6, 8, 45-52, 54, 55]). ТЕРМОЭЛЕКТРОДВИЖУЩАЯ СИЛА МЕТАЛЛОВ И СПЛАВОВ 2.1. МЕХАНИЗМ Т. Э. Д. С. В МЕТАЛЛАХ И СПЛАВАХ 2.1.1. ДИФФУЗИОННАЯ Т. Э. Д. С. Основной причиной возникновения т. э. д. с. в металлах и сплавах при создании в них градиента температуры является отклонение электронной системы от равновесия. Соответствующая т.э.д.с. называется диффузионной, поскольку ее можно рассматривать как результат диффузии носителей тока в поле градиента температуры. Диффузионная т. э. д. с. реального металла определяется механизмом или несколькими механизмами рассеяния носителей тока на фо-нонах, дефектах решетки, примесных атомах, магнонах (в магнито-упорядоченных металлах), границах зерен (в чистых металлах при низких температурах) и т. д., а также электронным спектром, в частности геометрией поверхности Ферми и температурой. Расчет т.э.д.с. на основе кинетического уравнения Больцмана дает выражения для т. э. д. с, которые часто используют для анализа экспериментальных данных и оценки влияния различных механизмов рассеяния на т. э. д. с: 5диф - 5диф = 2 tl Зе пЧ1 д\пр (е) дъ ,2 fc2 д\пт{е) д\пу din а (е) дв де. dim а In т (е) д 1п t) дЫЫ (е) ае дг д\пе (2.1а) (2.16) {2.1в) где е - заряд электрона; Т - абсолютная температура; е, т и ti - энергия, время релаксации и групповая скорость носителей тока; ер - энергия Ферми; Л'(е)-плотность состояний; 0(e)-площадь нзоэнергетической поверхности; кв - константа Больцмана и р - удельное электросопротивление. Уравнения (2.1) справедливы для идеального металла нли сплава с изотропным электронным спектром в случае упругого рассеяния электронов. Из уравнения (2.1а) видно, что в случае действия одного механизма рассеяния 5диф не должна зависеть от концентрации рассеивающих центров. В соответствии с уравнениями (2.1) 5диф должна быть линейной функцией температуры, что подтверждается экспериментальными данными для ряда металлов и сплавов при высоких температурах. Диффузионная т. э. д. с. доминирует в чистых металлах при высоких (r>9D, где Qd - температура Дебая) и промежуточных температурах; в не слишком разбавленных сплавах, т. е. при концентрации легирующих элементов от нескольких процентов и больше, она является основным механизмом т. э. д. с. прн всех темпе-р а тур ах. 2.1.2. Т.Э.Д.С. ФОНОННОГО УВЛЕЧЕНИЯ При низких температурах у ряда чистых металлов наблюдаются весьма сильные отклонения температурной зависимости S(T) от
Рнс. 2.1. Температурная завнснмость абсолютной т. э. д. с. золота [58]. бо - температура Дебая предсказанной уравнениями (2.1). Эти зависимости имеют вид широких максимумов и объясняются так называемым эффектом фо-ноиного увлечения, связанного с неравновесными условиями в фо-нонной системе. Если электрон-фононное взаимодействие не явля- ется пренебрежимо малым, то будет происходить перенос импульса от упорядоченного потока фононов к электронной системе, т. е. появится дополнительная движущая сила, создающая упорядоченное движение носителей тока (фононы как бы увлекают электроны за собой) и соответственно дополнительный вклад в т. э. д. с, именуемый т. э. д. с. фононного увлечения. Величина 5фон сначала растет при увеличении температуры вместе с увеличением равновесной концентрации фононов, а затем убывает за счет увеличения числа фонон-фононных столкновений, препятствующих передаче импульса электронам от фононной системы. В результате получается кривая 5фон(Г) с максимумом, положение которого определяется в основном фононным спектром металла; у многих металлов 0,109в^Гтах0,29в. Наиболее распространенное приближенное выражение для 5фон имеет вид: Sфoн~ac,/3/гe, (2.2) Где Cl - решеточная теплоемкость; п - концентрация электронов проводимости; е - заряд электрона; а - отношение числа электрон-фононных столкновений к общему числу столкновений фононов. Идеальная зависимость т.э.д.с. от температуры должна описываться кривой, подобной изображенной на рис. 2.1. Из выражения (2.2) видно, что любые источники рассеяния фононов -примеси дефекты приводят к уменьшению 5фон за счет уменьшения а. Практически уже при комнатной температуре т.э.д.с. фононного увлечения в металлах становится равной нулю. Соотношение (2.2), включающее отрицательный множитель 1/е, предсказывает отрицательные значения 5фон. Между тем большое число переходных и непереходных металлов (например, палладий, медь, золото и др.) и сплавов характеризуется положительными значениями 5фон. Положительный знак 5фон связывают с вкладом в т.э.д.с, помимо нормальных процессов элек-трон-фононного рассеяния, так называемых процессов переброса или и-процессов, при которых изменения волновых векторов близки к векторам обратной решетки, а также со сложной геометрией поверхности Ферми. Характерные максимумы 5фон у щелочных металлов иллюстрирует рис 2.2. 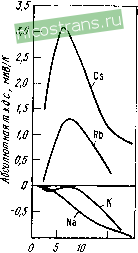 /5 Т,К Рис. 2.2. Абсолютная т.э.д.с. щелочных металлов при низких температурах [35] Имеются В виду атомы посторонних примесей илн легирующих элементов в сплавах. 2.1.3. Т. Э. Д. С. ПРИ НАЛИЧИИ НЕСКОЛЬКИХ МЕХАНИЗМОВ РАССЕЯНИЯ Приведенные выше выражения для т.э.д.с. (2.1) были получены в предположении существования в металлах одного механизма рассеяния электронов проводимости - электрон-фононного взаимодействия. Между тем в реальных металлах всегда существуют другие механизмы рассеяния - на дефектах решетки, на примесных атомах и т. д. Для описания т. э. д. с. при наличии двух механизмов рассеяния, например на фононах и примеси, используется правило Колера: 5-El!---АЕ 5прим (2.3) где Wo н S° -тепловое сопротивление и т.э.д.с. металла, не содержащего примесей; AW и S p - изменение теплового сопротивления и характеристическая т.э.д.с, связанные с примесями. При этом S P определяется выражением, аналогичным (2.1): прим . д 1п I Др (е) 1 (2.4) где Др - изменение сопротивления, связанное с данными примесями. В случае, если выполняется правило Маттисена и закон Виде-маиа-Франца, уравнение (2.3) переходит в: s=s - , ПРИ! Ро + Ар (2.5) Ро +Ар известное как правило Нордгейма - Гортера (ро-электросопротивление чистого металла). При достаточно низких температурах в области остаточного сопротивления, где po<SAp, т.э.д.с. металлов определяется исключительно рассеянием на доминирующей примеси или нескольких примесях, уравнения (2.3) и (2.5) легко обобщаются на случай нескольких механизмов рассеяния или типов рассеивающих центров. При этом в случае одной примеси в металле т. э. д. с. не зависит от се концентрации. При высоких температурах, если концентрации посторонних примесей в металле малы (Др<Сро), т.э.д.с. определяется рассеянием на фононах. 2.1.4. Т. Э. Д. С. ПРИ НАЛИЧИИ НЕСКОЛЬКИХ ТИПОВ НОСИТЕЛЕЙ ТОКА Приведенное выше относилось к простому случаю, когда вклад проводимости в металле осуществляется носителями одного типа. Между тем у ряда металлов в проводимости могут участвовать носители тока, принадлежащие нескольким зонам (например, электроны и дырки в переходных металлах) или несколько групп носителей тока, принадлежащих одной зоне, но соответствующие различным областям сильно анизотропной поверхности Ферми. В этом случае результируюп.;ая т. э. д. с. определяется выражением: (2.6) 19 где CTi и Si -электропроводность и т.э.д.с, соответствующие г-той группе носителей тока. Поскольку, как следует из приведенных выше формул, St для дырок должна быть положительной, то согласно выражению (2,6) с ростом концентрации дырок положительный вклад в т. э. д. с. должен расти, что существенно для ряда сплавов переходных металлов. 2.2. Т. Э.Д. С. МЕТАЛЛОВ 2.2.1. НЕПЕРЕХОДНЫЕ МЕТАЛЛЫ При высоких температурах (r Oi,) диффузионная т.э.д.с чистых металлов определяется электрон-фононным рассеянием. При этом в модели квазисвободных электронов для простейшей формы элект-рои-фононного взаимодействия из уравнения (2.1) следует: 5диф - (2.7) где Tf-температура Ферми (порядка 10К для простых металлов), определяемая соотношением квТр-ъ^. Величина ksje представляет собой фундаментальную т. э. д. с. электронов, равную -86 мкВ/К. У чистых металлов эксперименталь- 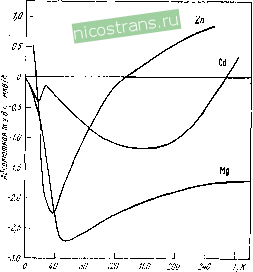 Рпс. 2.3. Абсолютная т. э. д. с. монокристаллов магния, цинка и кадмия 59]. Измерения параллельно главной кристаллографической оси но наблюдаемые величины т. э. д. с. более чем на порядок ниже этого значения из-за наличия в выражении (2.7) малого параметра или Т/Тр. При низких температурах (Г^б ) т.э.д.с ме-
талла может определяться рассеянием как на фононах, так и на посторонних примесях. Выражение (2.7), полученное на основе довольно грубых предположений и простых моделей, в ряде случаев позволяет правильно предсказать температурную зависимость и порядок величины т. э. д. с. непереходных металлов при высоких температурах. Так, согласно выражению (2.7) 5яиф при Г 300 К должна составлять несколько микровольт на Кельвин, что согласуется, например, с данными для поливалентных (Mg, Zn, Cd, рис. 2.3) или благородных (Си, Ag, Au, рис. 2.4) металлов. Однако при низких температурах (<10К) у благородных металлов наблюдаются завышенные на два порядка значения. Кроме того, согласно выражению (2.7) значения диффузионной т. э. д. с. для непереходных металлов со сферической поверхностью Фер- ми должны иметь отрицательный знак, тогда как у ряда металлов (например, у благородных Си, Ag, Au, некоторых поливалентных Са, Zn, Cd) наблюдаются положительные значения Здиф. Указанные расхождения в величинах и знаке т. э. д. с. связывают с несферичностью поверхности Ферми, анизотропией электронного рассеяния и электрон-электронным взаимодействием. У ряда металлов наблюдается несоответствие между экспериментально наблюдаемым (положительным) и предсказываемым теорией (отрицательным) знаками 5диф. В качестве примера можно привести данные для меди, серебра и золота, некоторых щелочных (см. рис. 2.2) и поливалентных (см. рис. 2.3) металлов. О причинах этого см, раздел 2.1.2. 2.2.2. ПЕРЕХОДНЫЕ МЕТАЛЛЫ Диффузионная т. э. д. с. Для переходных металлов характерна весьма высокая т. э. д. с. при повышенных температурах, достигающая 50 мкВ/К и значитель?го превосходящая соответствующую т. э. д. с. металлов с заполненными внутренними электронными оболочками (рис. 2.5). Большая отрицательная т. э. д. с. переходных металлов никеля, палладия и платины при температурах >300 К может быть описана в рамках модели Мотта. Согласно Мотту процессы проводимости в переходных металлах осуществляются в основном s-электронами, имеющими меньшую эффективную массу и более высокую подвижность, а в процессе рассеяния доминируют s-d-переходы. Последнее связано с высокой ft ft f t .РЬАиСаД; Си Al Рис. 2.4. Абсолютная т. э. д. с. некоторых поливалентных и благородных металлов (по совокупности литературны.х данных). Стрелками указаны температуры Дебая Одновалентные металлы подгруппы !б, плотностью состояний в d-зонах N(d), что приводит к большой вероятности S-d-рассеяния. Поскольку N(d) у переходных металлов сильно зависит от энергии, а уровень Ферми у никеля, палладия и платины сдвинут в сторону больших энергий от максимума на кривой Nd (е), первое слагаемое в выражении (2,1 в) обеспечивает большую отрицательную величину 5диф. У переходных металлов 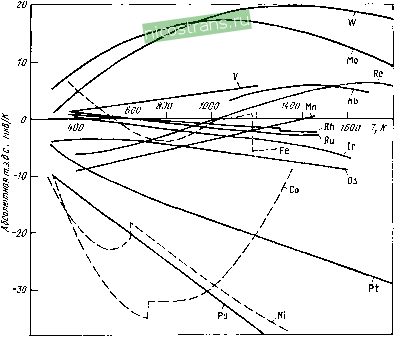 Рис. 2.5. Абсолютная т. э. д, с. некоторых переходных металлов (по совокупности литературных данных) группы хрома (хром, молибден, вольфрам) уровень Ферми сдвинут в сторону меньших энергий от максимума на кривых Nd (е) [или /V/ (е)]. Это должно приводить к положительной величине т.э.д.с, что согласуется с экспериментальными данными. Модель Мотта, несмотря иа лежащие в ее основе грубые допущения, позволяет весьма удовлетворительно описывать т. э. д. с. ряда переходных металлов при высоких температурах. Так, использование миогозонпого варианта модели Мотта для расчета температурных зависимостей т, э. д. с. палладия, платины, молибдена, вольфрама и других металлов позволило достичь хорошего качественного согласия с экспериментальными данными. Т. э. д. с. фононного и магнонного увлечения Величины максимумов фононного увлечения в переходных металлах приблизительно на порядок выше, чем в простых металлах, У ряда переходных металлов (например, платины, палладия, ниобия, тантала, рения) наблюдаются положительные максимумы фононного увлечения. Этот факт может быть связан с электрон-фононным S-а-рассеянием. Поскольку конечные состояния рассеиваемых s-электронов, попадающих в d-зопу, характеризуются высокой эффективной массой и, следовательно, малой скоростью электронов, при электрон-фононных столкновениях скорость электронов в направлении волнового вектора фонона, как правило, будет уменьшаться. В результате возникает обратное увлечение фононами (торможение), т.е. положительная т.э.д.с. фононного увлечения. Альтернативная гипотеза связывает положительный знак 5фои с вкладом дырочного рассеяния. В магнитоупорядочениых (ферромагнитных и антиферромагнитных) переходных металлах есть еще один механизм т. э. д. с. - т. э. д. с. магнонного увлечения. Магноиное увлечение связано с рассеянием электронов на спиновых волнах и представляет собой эффект, аналогичный увлечению электронов фононами. Согласно расчету при низких температурах 5магн должна меняться пропорционально Т^ в ферромагнетиках и Р в антнферромагнетиках. Установлено, что основной вклад в т. э. д. с, железа прн низких температурах вносит 5магн. Эффект магнонного увлечения играет большую роль в т.э.д.с. лантаноидов, являясь одной из причин немонотонной температурной зависимости прн низких температурах. 2.3. Т.Э.Д.С. СПЛАВОВ 2,3.1. СПЛАВЫ НА ОСНОВЕ НЕПЕРЕХОДНЫХ МЕТАЛЛОВ Сплавы не содержащие переходных 3 d-элементов Диффузионная т. э. д. с. При малых концентрациях легирующих элементов изменение т. э. д, с. металла в результате легирования обусловлено лишь появлением дополнительных центров (механизмов) рассеяния. В этом случае т. э, д. с, например двухкомпонентного сплава, описывается правилом Н о р д г е й м а-гГ о р т е р а (2.5), в соответствии с которым изменения т.э.д.с. в результате легирования пропорциональны Др. Из выражения (2.5) видно, что прн низких температурах (7<c9d, р Р * >Ро) в сплаве, содержащем один легирующий элемент г, т. э. д. с, не должна зависеть от концентрации этого элемента, так как р' л р,-. При промежуточных температурах зависимость 5(7 ) определяется конкуренцией процессов рассеяния на этом легирующем элементе н фононах. В приближении Нордгейма-Гортера направление изменения т. э. д. с. металла в результате легирования определяется знаком величины (S -Sf ), который трудно предсказать исходя из каких-либо априорных соображений. Можно сформулировать лишь некоторые эмпирические закономерности, справедливые для отдельных групп сплавов, в частности для сплавов с переходными металлами (см. 2.3.2). Т. э. д. с. фононного увлечения Влияние легирования на 5фон связано с двумя основными эффектами. Первый из них -подавление 5фои, обусловленное рассеянием фононов, вследствие разницы масс атомов матрицы и легирующих элементов, разницы силовых констант или поля напряжений вокруг чужеродных атомов. Этот эффект проявляется уже в разбавленных сплавах и приводит к тому, что во многих случаях 5фон практически равна нулю уже при концентрации примесей порядка 1 %. Примером подавления 5фон за счет разницы масс является поведение сплавов систем Си-Cd, Си-In, Си-Sn и Си-Sb, в которых при содержании легирующих элементов порядка 1 % фононный максимум исчезает. Второй эффект связан с искажением поверхности Ферми в результате легирования и с изменением ее положения относительно границы зоны Бриллюэна, что в свою очередь может изменить соотношение между нормальными Л^- и (/-процессами электрон-фонон-ного взаимодействия и в ряде случаев может привести даже к увеличению 5фон. Наблюдаемое увеличение фононного максимума при больших концентрациях легирующих элементов (~3-5%) в сплавах Си-Zn, Си-As, Си-Ga и Си-Ge объясняют приближением поверхности Ферми к граням {200} зоны Бриллюэна и соответствующим увеличением доли (/-процессов в рассеянии. Сплавы, содержащие переходные 3 d-металлы Аномально высокие значения т.э.д.с. при низких температурах, значительно превосходящие величины, предсказываемые формулами 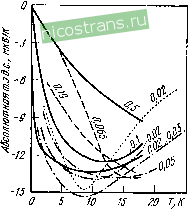 ч -10 -15
О 50 100 150 200 250 Т,К Рис. 2.6. Абсолютная т. э. д. с. сплавов Au-Fe при низких температурах. По литературным данным сопоставлено [41, с. 150-169]. Цифры у кривых - концентрация железа в сплавах, % (ат.) Рис. 2.7. Абсолютная т. э. д. с. сплавов Au-Со при низких температурах [60]. Цифры у кривых - концентрация железа в сплавах, % (ат.) (2.1), впервые были обнаружены у сплавов Au-Fe, Au-Со, Си-Fe и Си-Со (рис. 2.6-2.8). Было установлено также, что для этих сплавов характерно и наличие низкотемпературных минимумов сопротивления. Аномальные кинетические свойства этих сплавов обус- ловлены обменным (спиновым) рассеянием электронов проводимости на локализованных магнитных моментах или эффектом Кондо. В настоящее время установлено, что эффект Кондо и связанные с ним аномалии термоэлектрических свойств не ограничены областью низких температур, а могут наблюдаться в широком интервале температур вплоть до высоких в зависимости от так называемой температуры Кондо , которая для различных сплавов может колебать- 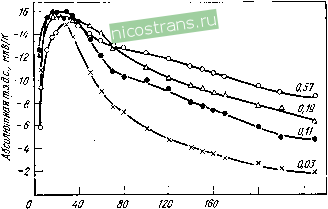 200 240 Т, К Рис. 2.8. Асболютная т. э. д. с. сплавов Си-Fe при низких температурах [61]. Цифры у кривых - концентрация железа в сплавах, % (ат.) СЯ от 10- до 10 К. Гигантская т.э.д.с, связанная с магнитными примесями, в настоящее время обнаружена также у сплавов серебра (Ag-Ре, Ag-Мп), золота п меди с другими Зй-металлами (Au-V, Ли-Мп, Си-V, Си-Мп), у сплавов на основе поливалентных металлов, например А1-Мп, а также у ряда сплавов на основе переходных металлов (см. 2.3.2). Гигантская т. э. д. с. наблюдалась также у некоторых трех-комнопентных сплавов, содержащих магнитные элементы. Примером могут служить сплавы на основе Си-Au, содержащие марганец, железо, кобальт, ванадий или никель, и сплавы на основе Си-А1, содержащие железо, а также сплавы, содержащие две магнитные примеси в одной медной матрице: Си-Ре-Со и Си-Ре-N1. Наибольшую т. э. д. с. среди сплавов указанного типа при низких температурах имеют сплавы Au-Fe и Си-Ре, а при промежуточных температурах - сплавы Au-Со и Си-Со. На кривых температурной зависимости т. э. д. с. разбавленных сплавов с магнитными примесями наблюдаются экстремумы, положение которых определяется видом сплава (величиной , а также содержанием легирующего элемента. Для сплавов на основе золота и меди температура максимума т. э. д. с. падает в ряду Ti-V-Cr (от ~ 10 К до ~1 К) и возрастает в ряду Fe--Co-*-->Ni (от ~ 10 К до -10 К). Можно отметить еще одну закономерность: элементы, стоящие слева от марганца в ряду Ti-Ni, изменяют т. э. д. с. золота и меди 1 2 3 4 ... 18 |
|||||||||||||||||||||||||||||||||